Gamifying the 2018 Olympic Games
Feb 06 2018
I love the Olympics and the upcoming 2018 Games have me fired up. Following my first season in a fantasy football league this year, I thought it would be a fun idea to try and make my own fantasy game for the Olympics. So with only a limited amount of knowledge of what makes a good fantasy game, I got to work on my own Fantasy Olympics.
One of the initial problems I foresaw with a game for the Olympics was the average person’s familiarity with individual athletes. While everyone knows the big stars (Michael Phelps, Shaun White, etc.), most viewers would probably struggle to name more than a handful of individual athletes. There is the same issue with fantasy football and defenses. In fantasy football, most leagues remedy this by having fantasy players draft whole defenses instead of individual defensemen and I thought a similar scheme would be a good solution for my own Fantasy Olympics problem.
So, instead of drafting a bunch of individual athletes, Fantasy Olympics players pick from teams of athletes by nationality and sport. For example, instead of drafting individual speed skaters, you might draft the speed skating team from the Netherlands (an excellent pick, given that they won 19 total medals at the Sochi games). You would then be awarded points for any medals won by any Dutch speed skaters.
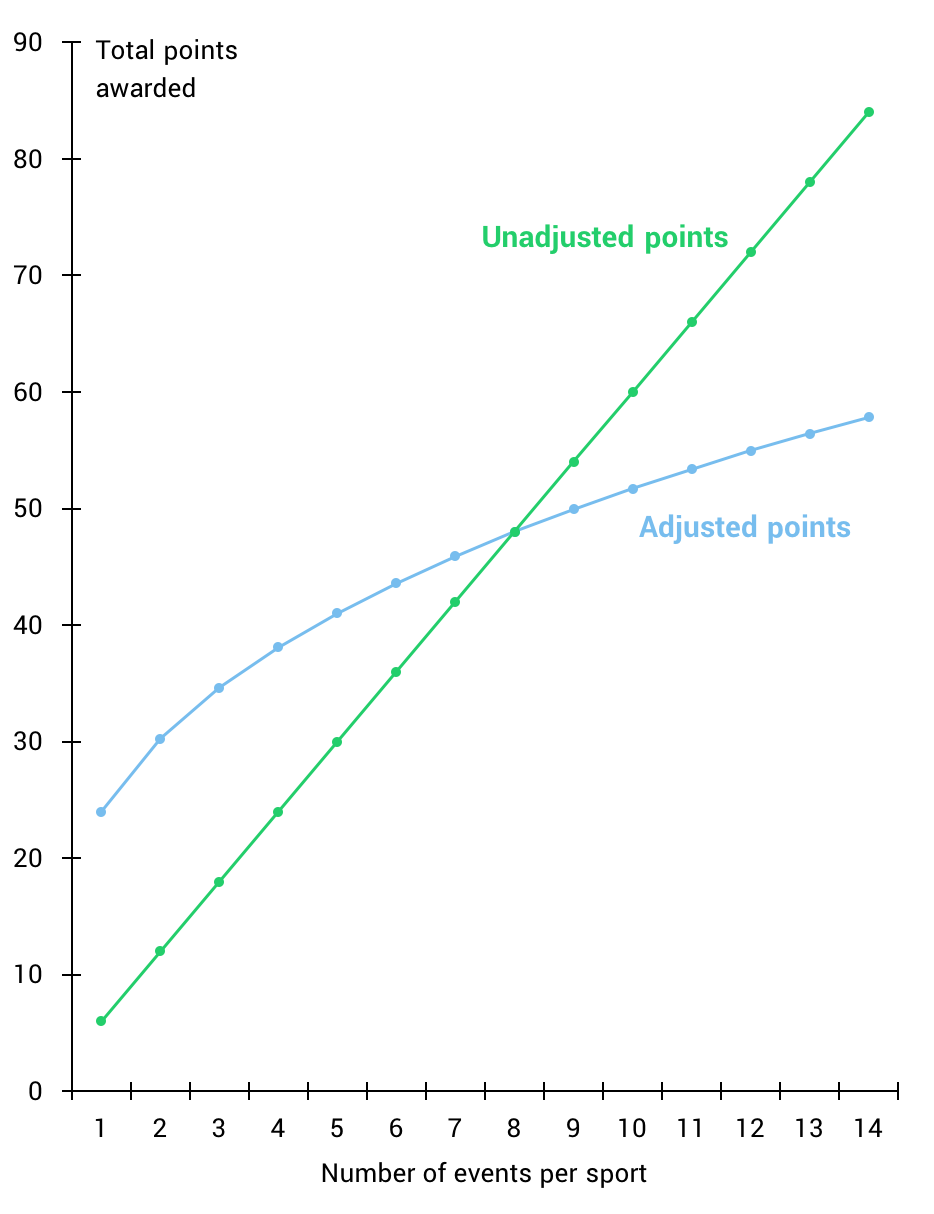
The next logical question: how many points are awarded per medal? The quickest and simplest scheme that comes to mind would be to award 3 points per gold, 2 points per silver, and 1 point per bronze. However, while simple, this scheme would offer a significant advantage to teams participating in sports with a large number of events. Using this scoring scheme, players would probably opt to pick a lower-skill alpine skiing team (with 11 total events to participate in) over an all-star hockey team (with only 2 total events to participate in).
In order correct for this, I decided to weight the scoring by how many events a particular sport has. Under my weighted scoring scheme, for each medal, a player is awarded $p = 4p_0 \frac{\sqrt[3]{x}}{x}$ points, where $x$ is the number of events in that particular sport and $p_0$ is either 3 for a gold medal, 2 for a silver medal, and 1 for a bronze medal. For example, if you had drafted the U.S. snowboarding team and Shaun White were to (does) win a gold, you would be awarded $4 * 3 * \frac{\sqrt[3]{10}}{10} = 2.6$ points, since there are 10 total snowboarding events. See below for the full medal breakdown by sport.
Using this scoring scheme, we get the point distribution seen on the right. As a result, a team that can compete in 3 events is not hugely disadvantaged in comparison to a team that can compete in 6 events. This should (ideally) move the focus away from the number of events a team can participate in and towards the skill of a particular team.
Fantasy Points Won per Medal by Sport
| Sport | Number of events | Points per gold | Points per silver | Points per bronze | Total points awarded |
|---|---|---|---|---|---|
| Alpine Skiing | 11 | 2.4 | 1.6 | 0.8 | 53.4 |
| Biathlon | 11 | 2.4 | 1.6 | 0.8 | 53.4 |
| Bobsleigh | 3 | 5.8 | 3.9 | 1.9 | 34.6 |
| Cross-Country Skiing | 12 | 2.3 | 1.5 | 0.8 | 55.0 |
| Curling | 3 | 5.8 | 3.9 | 1.9 | 34.6 |
| Freestyle Skiing | 10 | 2.6 | 1.7 | 0.7 | 51.7 |
| Figure Skating | 5 | 4.1 | 2.7 | 1.4 | 41.0 |
| Ice Hockey | 2 | 7.6 | 5.0 | 2.5 | 30.2 |
| Luge | 4 | 4.8 | 3.2 | 1.6 | 38.1 |
| Nordic Combined | 3 | 5.8 | 3.9 | 1.9 | 34.6 |
| Skeleton | 2 | 7.6 | 5.0 | 2.5 | 30.2 |
| Ski Jumping | 4 | 4.8 | 3.2 | 1.6 | 38.1 |
| Speed Skating | 14 | 2.1 | 1.3 | 0.7 | 57.8 |
| Short Track Speed Skating | 8 | 3.0 | 2.0 | 1.0 | 48.0 |
| Snowboarding | 10 | 2.6 | 1.7 | 0.7 | 51.7 |
With these questions answered, Fantasy Olympics was ready to be played! But besides just setting the rules of the game, I was curious to see how accurate of projections I could make. Everyone’s trying to come up the perfect fantasy football predictions so I thought I’d get a head start on the projection game for when Fantasy Olympics inevitably blows up.
For my projections, I went with a fairly straight forward regression based on each team’s historical performances. Since there is a long gap between each of the Games, I had to consider how much historical data to include or not include in my regression. I opted to use a mean regression based on the five previous games (meaning data back to 1998 to predict the 2018 Games). This model seemed to fare best when testing against previous Games, but we shall see how it fares for these Games. See below for my full projections by country and sport.
Projected Fantasy Points by Country and Sport
| Country | Alpine Skiing | Biathlon | Bobsleigh | Cross-Country Skiing | Curling | Figure Skating | Freestyle Skiing | Ice Hockey | Luge | Nordic Combined | Skeleton | Ski Jumping | Snowboard | Speed Skating | Short Track Speed Skating | Total |
|---|
← Scroll →
← Scroll →
Based on these 182 total projections, the top five picks would be the German Luge team (16.14 points), the Dutch Speed Skating team (15.89 points), the Canadian Ice Hockey teams (13.41 points), the Norwegian Cross-Country Skiing team (13.08 points), and the Korean Short Track Speed Skating team (12.64 points). Based purely on my knowledge from past Olympics, these projections seem fairly accurate, which is a good sign. The Dutch speed skaters crushed in Sochi, Germany is always a top luge contender, and, I mean, it’s Canada and hockey.
The United States is the top overall projected country, but we shall see if that proves to be correct. Sochi was a bit of a disappointment for the U.S. team, coming in fourth for overall medals, though Vancouver was a bit better. Let’s hope they can pull it out in South Korea.
Regardless of who wins and how accurate these projections end up being, I’m excited to watch two weeks of the best in sport. But also, go USA!